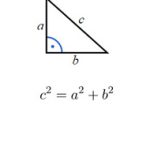
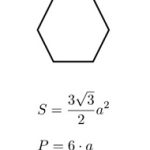
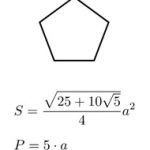
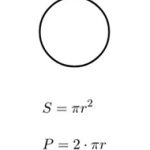
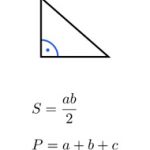
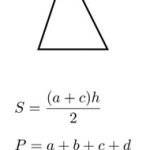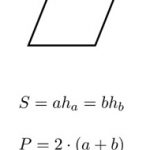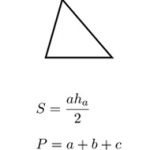- Đa giác đều là một hình học hai chiều có tất cả các cạnh bằng nhau và các góc ở đỉnh bằng nhau.
Tính chu vi. Chu vi là tổng chiều dài các mặt ngoài của bất kỳ hình học phẳng. Với một đa giác đều, chu vi có thể được tính bằng cách nhân chiều dài một cạnh với số cạnh (n)
Xác định đường trung đoạn. Đường trung đoạn của một đa giác đều là đoạn thẳng vuông góc hạ từ tâm xuống một cạnh của nó. Đường trung đoạn hơi khó để tính hơn một chút so với chu vi.
- Công thức tính độ dài đường trung đoạn là: độ dài cạnh (s) chia cho tất cả 2 lần (tan) của thương số 180 độ và số cạnh (n).
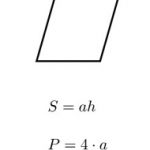
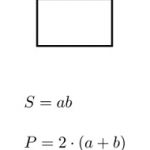
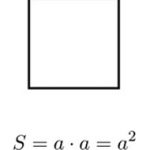
Diện tích của bất kỳ đa giác đều nào cũng được tính bằng công thức:Diện tích = (a x p)/2, trong đó, a là độ dài đường trung đoạn và p là chu vi đa giác đó.
Các công thức
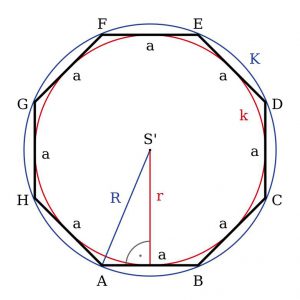
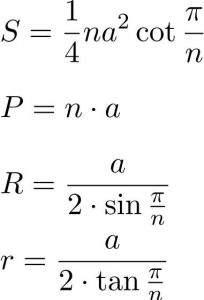
- P – chu vi
- S – diện tích
- R – bán kính K
- r – bán kính k
- n – số cạnh
- S’ – tâm
- a – các cạnh
- K – đường tròn ngoại tiếp
- k – đường tròn nội tiếp
Đường tròn ngoại tiếp của một đa giác là một đường tròn đi qua tất cả các đỉnh của đa giác.
Đường tròn tiếp xúc với tất cả các cạnh của một đa giác được gọi là đường tròn nội tiếp đa giác và đa giác được gọi là ngoại tiếp đường tròn.